Take out a sheet of paper. Pop quiz! (just kidding).
Draw any number of dots on your page. Now connect the dots with lines, subject to the following rules: lines may not cross each other as they move from dot to dot, and every dot on your page must be connected to every other dot through a sequence of lines.
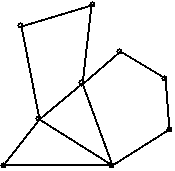
Now count the number dots (D), lines (L), and regions separated by lines (R). (Don’t forget to count the outside as a region too.) Compute D-L+R. What do you get?
No matter how you started, the number you will always get is 2!
In the figure, D=9, L=12, R=5, and indeed, D-L+R=2.
If the lines represent fences, and the dots fenceposts, then the regions separated by the fenceposts are the pastures. So, if you are a farmer who wants to fence off 4 pastures together with 55 sections of fence, you can calculate exactly how many fenceposts you need, no matter how you arrange the fences!
(L=55, R=5=4+outside, so D=2+L-R=2+55-5=52 fenceposts.)
Presentation Suggestions:
You may wish to have everyone shout out their answer at the same time… students will be surprised they all get the same answer.
The Math Behind the Fact:
The number D-L+R is called the Euler characteristic of a surface. It is an invariant of a surface, meaning that while it looks like it may depend on the system of fences you draw, it really does not (as long as every pasture, including the outside, is topologically a disk with no holes). Thus the number only depends on the topology of the surface that you are on! For planes and spheres, this number is always 2.
How to Cite this Page:
Su, Francis E., et al. “Euler Characteristic.” Math Fun Facts. <http://www.math.hmc.edu/funfacts>.
Fun Fact suggested by:
Francis Su

