You know the formula for the area of a circle of radius R. It is Pi * R2.
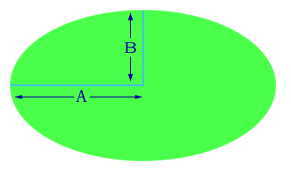
But what about the formula for the area of an ellipse of semi-major axis of length A and semi-minor axis of length B? (These semi-major axes are half the lengths of, respectively, the largest and smallest diameters of the ellipse.)
For example, the following is a standard equation for such an ellipse centered at the origin: (x2 / A2) + (y2 / B2) = 1.
The area of such an ellipse is Area = Pi * A * B ,
a very natural generalization of the formula for a circle!
Presentation Suggestions:
If students guess this fact, ask them what they think the volume of an ellipsoid is!
The Math Behind the Fact:
One way to see why the formula is true is to realize that the above ellipse is just a unit circle that has been stretched by a factor A in the x-direction, and a factor B in the y-direction. Hence the area of the ellipse is just A*B times the area of the unit circle.
The formula can also be proved using a trigonometric substitution. For a more interesting proof, use line integrals and Green’s Theorem in multivariable calculus.
Each of the above proofs will generalize to show that the volume of an ellipsoid with semi-axes A, B, and C is just (4/3) * Pi * A * B * C.
(Just think of a stretched sphere, use trig substitution, or use an appropriate flux integral.)
By the way, unlike areas, the formula for the length of the perimeter of a circle does not generalize in any nice way to the perimeter of an ellipse, whose arclength is not expressible in closed form— this difficulty gave rise to the study of the so-called elliptic integrals.
How to Cite this Page:
Su, Francis E., et al. “Area of an Ellipse.” Math Fun Facts. <http://www.math.hmc.edu/funfacts>.
References:
For more fun with geometry, see Coxeter and Greitzer, Geometry Revisited.
Fun Fact suggested by:
Francis Su

