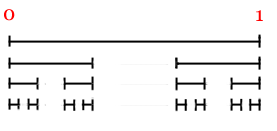
Start with the interval [0,1]. Remove the (open) middle third of it, i.e. get (1/3, 2/3). Now remove the middle thirds of each of the remaining intervals, i.e. get (1/9, 2/9) and (7/9, 8/9). Continue this process ad infinitum. The points left over form a fractal called the standard Cantor Set. It is an infinite set since a lot of points, including the endpoints of the removed intervals, are never removed. Can you list the endpoints?
Now let’s think about lengths. The length of the original interval is 1. Now how much “length” do we remove during the process?
At the first step, we remove an interval of length 1/3. At the second step, we remove two intervals of length 1/9. At the third step, we remove 4 intervals with total length 1/27, etc. What is the total length removed during the entire process? A geometric series! SUM1 to infinity (2n-1/3n) = 1.
Wait a minute … you mean we have an infinite set left over with 0 length??
Yes, and it’s worse than that: the set is uncountable! Thus it has as many points as interval that we started with!
Presentation Suggestions:
Use this Fun Fact after students learn to sum geometric series. You may wish to assign the sum of the lengths “removed” as an exercise before presenting this Fun Fact. (Of course, you can also do the computation in terms of how much remains after each stage and get a limiting sequence instead.) Follow with the Fun Fact Devil’s Staircase.
The Math Behind the Fact:
The real numbers are far stranger than any of your students might have suspected! The standard Cantor Set is quite interesting: it is an uncountable, totally disconnected, perfect (every point is a limit point) set of “Lebesgue measure zero”. Another way to describe the standard Cantor Set is the set of all real numbers in [0,1] expressible without 1’s in its base 3 expansion! Though first constructed as a pathological example, it arises naturally as a fractal in the study of dynamical systems.
How to Cite this Page:
Su, Francis E., et al. “Cantor Set.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
References:
Any text on real analysis.
Fun Fact suggested by:
Joshua Sabloff

