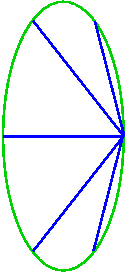
Consider N equally spaced on points on the unit circle, with the point P=(1,0) as one of these equally spaced points, and draw (N-1) chords from P to every other point. In Chords of a Unit Circle, we saw that the product of the lengths of these chords was just N. But what happens if we stretch this circle so that it is an ellipse?
For instance, suppose we consider the unit circle (with chords drawn from P to N-1 equally spaced points on the circle), and now scale the vertical direction by Sqrt[5], so that the circle becomes an ellipse, elongated vertically (and the points where chords meet the ellipse are no longer equally spaced along the ellipse). Note that the chords lengthen under this scaling. What is the product of the lengths of the chords?
Surprisingly, it is just N times the N-th Fibonacci number!
Presentation Suggestions:
Recall that the N-th Fibonacci number FN is defined by F1=F2=1, and each FN=FN-1+FN-2.
The Math Behind the Fact:
The reference proves that for an ellipse of semi-major axis A+B and semi-minor axis A-B, the product of the lengths of the chords described above is just N times the quantity (AN – BN)/(A-B). But this latter expression becomes Binet’s formula for Fibonacci numbers if A is the golden mean (1+Sqrt[5])/2 and B is the complementary golden number (1-Sqrt[5])/2. In that case A+B=1, and A-B=Sqrt[5], giving the dimensions of the ellipse needed to make the Fact true!
How to Cite this Page:
Su, Francis E., et al. “Chords of an Ellipse.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
References:
Thomas Price, “Products of Chord Lengths of an Ellipse”, Mathematics Magazine, 74(2002), 300-307.
Fun Fact suggested by:
Tom Price

