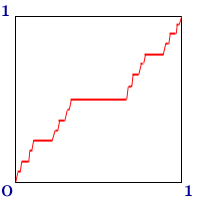
Here is a strange continuous function on the unit interval, whose derivative is 0 almost everywhere, but it somehow magically rises from 0 to 1!
Take any number X in the unit interval, and express it in base 3. Chop off the base 3 expansion right after the first 1. Next change all 2’s in the expansion to 1’s. This number now has only 0’s or 1’s in its expansion, so we can interpret it as a base 2 number! Call this new number f(x).
If you plot this function, you get something called the Devil’s Staircase. It is related to the standard Cantor set in the following way. This function is constant at all the removed intervals from the standard Cantor set. For instance if x is in [1/3, 2/3], then f(x)=1/2. If x is in [1/9, 2/9], then f(x)=1/4; if x is in [7/9, 8/9], then f(x)=3/4.
If you plot this you will see that this function is not differentiable at the Cantor set points, but has zero derivative everywhere else! But since a Cantor set has measure zero, this function is has zero derivative practically everywhere, and only “rises” on Cantor set points!
Presentation Suggestions:
Draw a good approximation to the devil’s staircase.
The Math Behind the Fact:
Pathological functions such as this one are important and fun examples that are studied in a real analysis course. Another fun pathology is a Continuous but Nowhere Differentiable function.
How to Cite this Page:
Su, Francis E., et al. “Devil’s Staircase.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
Fun Fact suggested by:
Lesley Ward

