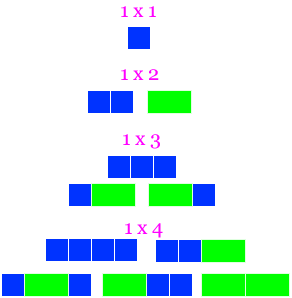
How many ways can you tile a (1 x n) board with (1 x 1) squares and (1 x 2) dominoes?
Let’s see…
A (1 x 1) board can only be tiled 1 way.
A (1 x 2) board can be tiled 2 ways: either two squares or one domino.
A (1 x 3) board can be tiled 3 ways: three squares, or a domino-square, or a square-domino.
A (1 x 4) board can be tiled 5 ways…
Hey, they are all Fibonacci numbers! These are numbers you get when you start a sequence 0 and 1 and generate the next sequence member by adding the previous two numbers: i.e., 0, 1, 1, 2, 3, 5, 8, …
Presentation Suggestions:
Draw pictures, and have students count the number of tilings themselves.
The Math Behind the Fact:
The Fibonacci property can be seen by conditioning on whether the first tile is a square or domino: the number of tilings where the first tile is a square is the number of ways to tile the remaining (n-1)-length board, and the number of tilings where the first tile is a domino is the number of ways to tile the remaining (n-2)-length board. A generalization of this idea can be used to develop combinatorial interpretations for many “Gibonacci” identities (recurrences in which the first terms are not necessarily 1 and 1); see the Benjamin-Quinn-Su reference for more on this.
An alternate generalization asks how many ways to tile an (m x n) board with dominoes; note that the (2 x n) case is equivalent to tiling a (1 x n) board with squares and dominoes. See the Graham-Knuth-Patashnik reference.
Other generalizations can be found in the Brigham-Caron-Chinn-Grimaldi reference. If you like this Fun Fact, you’ll like all the stuff that is in the Benjamin-Quinn book in the references.
How to Cite this Page:
Su, Francis E., et al. “Domino and Square Tilings.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
References:
A. Benjamin, J. Quinn, and F. Su, “Phased Tilings and Generalized Fibonacci Identities”, Fibonacci Quarterly, 2000.
Brigham, Caron, Chinn and Grimaldi, “A Tiling Scheme for the Fibonacci Numbers”, J. Recreational Math, 28(1), 1996-7, pp. 10-17.
Graham, Knuth, Patashnik, Concrete Mathematics, Section 7.1. Benjamin and Quinn, Proofs that Really Count.
Fun Fact suggested by:
Arthur Benjamin

