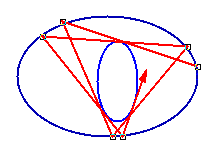
Given an ellipse, and a smaller ellipse strictly inside it, start at a point on the outer ellipse, and in a counterclockwise fashion (say), follow a line tangent to the inner ellipse until you hit the outer ellipse again. Repeat. Figure 1 shows an example.
Now it is quite possible that this path will never hit the same points on the outer ellipse twice. But if it does “close up” in a certain number of steps, then something amazing is true: all such paths, starting at any point on the outer ellipse, close up in the same number of steps!
This fact is known as Poncelet’s Theorem.
Presentation Suggestions:
Intuition may be gained by presenting special cases, such as where the ellipses are concentric circles.
The Math Behind the Fact:
This process that produces this path may be thought of as a dynamical system on the outer ellipse, and is related to the study of circle maps and rotation numbers in dynamical systems. You can learn more about Poncelet’s theorem in any classical text on algebraic geometry.
How to Cite this Page:
Su, Francis E., et al. “Ellipsoidal Paths.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
Fun Fact suggested by:
Jorge Aarao, Johannes Huisman

