Say you and a friend wish to share a cake. What is a “fair” way to split it? Probably you know this solution: one cuts, the other chooses. This is called a fair division algorithm, because by playing a good strategy, each player can guarantee she gets at least 50 percent of the cake in her own measure. See if you can reason why.
Now, what about for 3 people? Is there an algorithm that guarantees each person what she feels is the largest piece? Such a division is called an envy-free division. Here is a procedure due to Selfridge and Conway. We mark strategies [in brackets]. Suppose the players are named Alice, Betty, Chuck.
- Alice cuts [into what she thinks are thirds].
- Betty trims one piece [to create a 2-way tie for largest], and sets the trimmings aside.
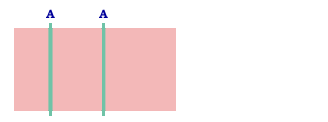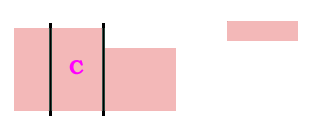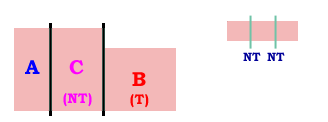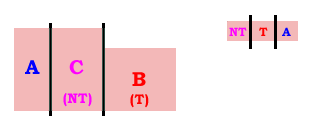
- Let Chuck pick a piece, then Betty, then Alice. Require Betty to take a trimmed piece if Charlie does not. Call the person who tooked the trimmed piece T, and the other (of Betty and Chuck) NT.
- To deal with the trimmings, let NT cut them [into what she thinks are thirds].
- Let players pick pieces in this order: T, Alice, then NT.
Presentation Suggestions:
Be sure you follow the argument before you present it, because it can be confusing! Draw pictures.
The Math Behind the Fact:
It is a good exercise to verify why each person is envy-free by the end of the procedure. The key observation is that for the trimmings, Alice has an “irrevocable advantage” with respect to T, since Alice will never envy T even if T gets all the trimmings. Thus Alice can pick after T, and this allows the procedure to terminate in a finite number of steps. For 4 or more players, there is an envy-free solution that is very complex, and can take arbitrarily long to resolve. See the references.
There are other notions of fairness besides envy-freeness. Proportional fairness is weaker; it only demands each person gets what she feels is at least 1/N of the cake. You might enjoy figuring out an N-person proportional procedure.
Questions of fairness are considered by mathematicians and economists in the subject of game theory.
How to Cite this Page:
Su, Francis E., et al. “Envy-free Cake Division.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
References:
S.J. Brams and A.D. Taylor, Fair Division: from cake-cutting to dispute-resolution, Cambridge, 1996.
J. Robertson and W. Webb, Cake-cutting Algorithms, AK Peters, 1998.
Fun Fact suggested by:
Francis Su

