One challenge in robotics is the problem of computer vision: how do you program a computer to interpret and “understand” the data it receives from some visual sensor? For example, one aspect of this problem is object recognition, and another is object tracking.
While recognition is a very hard problem (that won’t concern us here), if you know what an object looks like, it can be tracked using some interesting mathematical ideas.


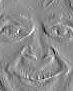
Suppose you are trying to track the face in Figure 1 as it moves in a sequence of frames. The visual data in each frame is an array of numbers (pixel intensities). Naively, you might track the face by searching each frame for an pattern of numbers similar to the one in Figure 1. But this can be very computationally intensive.
Here is a better method used by computer scientists. The key idea is linearization— while an object’s motion may not be linear, for small time steps it is approximately linear. So we would expect that the frames alter in approximately linear ways.
And they do! In the first row of Figure 2, we see a face moving left in a sequence of frames (look at them right-to-left). We can approximate the motion by looking at the frame in the first row labeled “+1 pix” and “subtracting” the original frame. This difference is shown in Figure 3. (If you like, you can think of it as a “derivative” representing the face’s motion!) If we assume that the face’s true motion is just the motion in Figure 3 repeated over and over, we get the approximation in the second row of Figure 2! As you can see, it remains a pretty good approximation for small numbers of steps. So we can “track” the face using this idea, as described below.
The Math Behind the Fact:
In practice, the array of pixel intensities is encoded as a (very long) vector of numbers. The space of all possible pictures forms a vector space, and the vector associated with Figure 2 forms a vector V. Tracking an object then correponds to finding the component of a given vector (picture) in the direction of V, and the multiple of V tells us the amount of the translation! Other motions can also be treated in this way, such as shifts up/down, rotation, scalings, etc. These correspond to vector components in other directions. (Thanks to Zach Dodds for providing the pictures, and Ran Libeskind-Hadas for providing his face!)
You can study linearity and vector spaces in a linear algebra course.
How to Cite this Page:
Su, Francis E., et al. “Face Derivatives and Computer Vision.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
Fun Fact suggested by:
Zach Dodds

