You are abducted by space aliens and dumped, blindfolded, on a strange asteroid! Removing your blindfold, you decide to play “Columbus” by walking in one direction forever to see if you can determine whether your asteroid is flat or curved. But you leave a trail of bread crumbs as you go, just in case you get lost.
After a few hours, you return to where you started, and rejoin the trail of bread crumbs.
You think to yourself, OK, this asteroid is curved and probably not planar. But then a crazy thought enters your mind— maybe the asteroid is shaped like a doughnut instead of a sphere? What experiment could you perform to tell the difference?
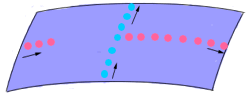
You decide to walk off in a transverse direction, leaving a trail of cheese crumbs this time. Suppose that after a long time you return to your original starting point, and your cheese crumbs never crossed the trail of bread crumbs except when you returned. What could you infer now?
Presentation Suggestions:
Pause and see if students can figure out what experiment to perform to tell the difference between a doughnut and a sphere. Draw a few plausible pictures of a sphere or a doughnut, and how our abducted explorer could have traveled.
The Math Behind the Fact:
Since any two “loops” (trails of crumbs) on a sphere which start and end at the same point must cross somewhere in between, you cannot be living on a sphere. It could be a doughnut(torus) or some other surface with more “holes”.
Mathematicians often study surfaces by their intrinsic properties. One way to study a surface is to study the set of all loops in the surface; this is called the fundamental group and it has an algebraic structure! You can add loops by concatenation, and two loops are “equal” if one can be deformed to the other. It turns out the the fundamental group is “topologically invariant”: it does not change if you deform the surface. So you can tell two surfaces are not topologically equivalent if they do not have the same fundamental group!
This is a fundamental idea in the field of topology. See also Mug Trick.
How to Cite this Page:
Su, Francis E., et al. “Fundamental Group.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
References:
Any text on algebraic topology
Fun Fact suggested by:
Francis Su

