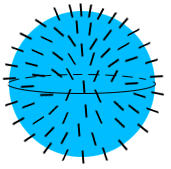
Another fun theorem from topology is the Hairy Ball Theorem. It states that given a ball with hairs all over it, it is impossible to comb the hairs continuously and have all the hairs lay flat. Some hair must be sticking straight up!
A more formal version says that any continuous tangent vector field on the sphere must have a point where the vector is zero.
Is the same true on a torus?
Presentation Suggestions:
Draw a picture of a sphere on the board, and have students think together with you how trying to draw a non-zero vector field would cause “problem points”, where the field is not continuous.
The Math Behind the Fact:
If you’ve done the Fun Fact on the Euler characteristic, students will find it very surprising that the number of “problem points” of a vector field on a surface is related to the Euler characteristic of that surface! Namely, every point has an “index” that describes how many times the vector field rotates in a neighborhood of the problem point. The sum of the indices of all the vector fields will be the Euler characteristic. Since the torus has Euler number 0, it is possible to have a vector field on it without any “problem points”.
A related Fun Fact is the Ham Sandwich Theorem.
How to Cite this Page:
Su, Francis E., et al. “Hairy Ball Theorem.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
Fun Fact suggested by:
Francis Su

