In the Fun Fact on Spherical Geometry, we saw an example of a space which is curved in such a way that the sum of angles in a triangle is greater than 180 degrees, where the sides of the triangle are “intrinsically” straight lines, or geodesics.
Is it also possible to have a space that “curves” in such a way that the sum of angles in a triangle is less than 180 degrees?
Yes! For instance, consider a saddle-shaped surface. A triangle that extends over the saddle of this surface (whose edges are geodesics) will have this property.
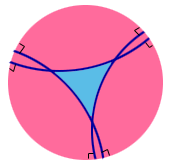
Another space with this property is something called the hyperbolic plane. This can be modeled by disc in which is “curved” in such a strange way that a bug on this disc would think that the “straight” lines are the pieces of circles or straight lines (viewed in planar geometry) that intersect the disc boundary at right angles. Any 3-sided figure using such lines will have angles in the corners that sum to less than 180 degrees!
Presentation Suggestions:
Convince students of the triangle assertion by drawing a saddle-shaped surface and a triangle on it. Alternatively, you could show that the angles of a square do not add to 360 degrees. Follow by showing drawing the hyperbolic disc and explaining what the “straight lines” are. You can also construct and bring to class an approximate physical model of a hyperbolic plane; the references discuss ways to construct them.
The Math Behind the Fact:
These spaces are examples of spaces with a kind of non-Euclidean geometry called hyperbolic geometry. Unlike planar geometry, the parallel postulate does not hold in hyperbolic geometry. Two lines are said to be parallel if they do not intersect. In Euclidean geometry, given a line L there is exactly one line through any given point P that is parallel to L (the parallel postulate). However in hyperbolic geometry, there are infinitely many lines parallel to L passing through P.
Mathematicians sometimes work with strange geometries by defining them in terms of a Riemannian metric, which gives a local notion of how to measure “distance” and “angles” on an arbitrary set. You can learn more about such metrics by taking a first course on real analysis, then following with an advanced course in differential geometry.
How to Cite this Page:
Su, Francis E., et al. “Hyperbolic Geometry.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
References:
J. Weeks, The Shape of Space, 1985.
D. Henderson, Experiencing Geometry in Euclidean, Spherical, and Hyperbolic Spaces, 2000.
Fun Fact suggested by:
Lesley Ward

