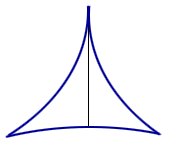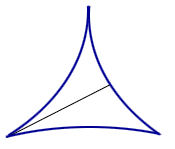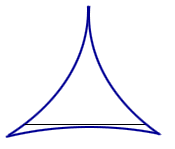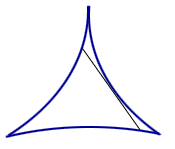
What is the smallest-area convex set in the plane inside which a needle (unit straight line segment) can be reversed (spun around 180 degrees)?
Answer: an equilateral triangle of unit height.
OK, now what if you allow non-convex sets? What is the smallest area set in which you can reverse a needle?
For instance, try a smaller 3-cusped hypercycloid. See Figure 1. In fact, you can try a similar idea with n-cusps. Suprisingly, there exists sets of arbitrarily small area in which a needle can be reversed!
Presentation Suggestions:
Draw pictures. Have people think about the second question for a minute.
The Math Behind the Fact:
This Fun Fact is easy to present but involves some deep mathematics. The construction of arbitrarily “small” sets (sets of small measure) containing a needle in all directions is a detailed analytical construction, and the general study of Kakeya sets is currently an active area of research in analysis. You can learn more about measure theory after taking a course in real analysis.
How to Cite this Page:
Su, Francis E., et al. “Kakeya Needle Problem.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
References:
E. Stein, Harmonic Analysis. MAA film; Falconer, p. 95.
Fun Fact suggested by:
Lesley Ward

