
A magic square is an NxN matrix in which every row, column, and diagonal add up to the same number. Ever wonder how to construct a magic square?
A silly way to make one is to put the same number in every entry of the matrix. So, let’s make the problem more interesting— let’s demand that we use the consecutive numbers.
I will show you a method that works when N is odd. As an example, consider a 3×3 magic square, as in Figure 1. Start with the middle entry of the top row. Place a 1 there. Now we’ll move consecutively through the other squares and place the numbers 2, 3, 4, etc. It’s easy: after placing a number, just remember to always move:
The only thing you must remember is to imagine the matrix has “wrap-around”, i.e., if you move off one edge of the magic square, you re-enter on the other side.
Thus in Figure 1, from the 1 you move up/right (with wraparound) to the bottom right corner to place a 2. Then you move again (with wraparound) to the middle left to place the 3. Then you cannot move up/right from here, so move down to the bottom left, and place the 4. Continue…
It’s that simple. Doing so will ensure that every square gets filled!
Presentation Suggestions:
Do 3×3 and 5×5 examples, and then let students make their own magic squares by using other sets of consecutive numbers. How does the magic number change with choice of starting number? How can you modify a magic square and still leave it magic?
The Math Behind the Fact:
See if you can figure out (prove) why this procedure works. Get intuition by looking at lots of examples!
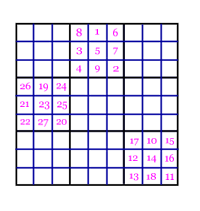
If you are ready for more, you might enjoy this variant: take a 9×9 square. You already know how to fill this with numbers 1 through 81. But let me show you another way! View the 9×9 as a 3×3 set of 3×3 blocks! Now fill the middle block of the top row with 1 through 9 as if it were its own little 3×3 magic square… then move to the bottom right block according to the rule above and fill it with 10 through 27 like a little magic square, etc. See Figure 2. When finished you’ll have a very interesting 9×9 magic square (and it won’t be apparent that you used any rule)!
How to Cite this Page:
Su, Francis E., et al. “Making Magic Squares.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
References:
The old Encyclopedia Brittanica has a wonderful and detailed article on the history and construction of magic squares!
See also W.S. Andres, Magic Squares and Cubes.
Fun Fact suggested by:
Francis Su

