A lattice point in the plane is any point that has integer coordinates.
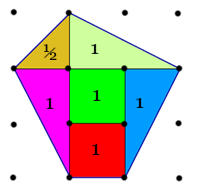
Let P be a polygon in the plane whose vertices have integer coordinates. Then the area of P can be determined just by counting the lattice points on the interior and boundary of the polygon!
In fact, the area is given by
Area(P) = i + (b/2) – 1
where i is the number interior lattice points, and b is the number of boundary lattice points.
Presentation Suggestions:
A neat application of Pick’s Theorem is that you cannot draw an equilateral triangle whose vertices lie on the lattice points.
Ask the students to try, making the point that the base does not need to be horizontal. Some convincing approximations may be obtained, but explain that none of them is really equilateral. This is true because the area of an equilateral triangle of base A is an irrational multiple of A2. If it is drawn on the lattice, then A2 is an integer —use the Pythagorean theorem— and the area is irrational, contradicting Pick’s theorem. (That’s also a good opportunity to prove that the square root of 3 is irrational.)
The Math Behind the Fact:
Pick’s theorem is non-trivial to prove. Start by showing the theorem is true when there are no lattice points on the interior.
How to Cite this Page:
Su, Francis E., et al. “Pick’s Theorem.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
References:
Ross Honsberger, Ingenuity in Mathematics.
Fun Fact suggested by:
Alon Amit

