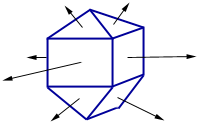
A polyhedron is any closed region of 3-space cut out by a finite set of planes.
Take any polyhedron and do the following: on each face, place a vector perpendicular to that face with length proportional to the area of that face.
No matter what polyhedron you started with, the sum of all those face vectors will be zero!
Presentation Suggestions:
First draw several polyhedra, and make sure some of them are very irregular. They do not even have to be convex… this fact is most surprising for the irregular polygons. Draw the face vectors so that students can see what you mean.
The Math Behind the Fact:
This Fun Fact can be proved by first showing that is is true for any tetrahedron. Use vector geometry to do this; express the face vectors in terms of the cross product of co-incident sides… when you sum them, everything will cancel. Since any polyhedron can be built up by tetrahedra, and since the sums of the face vectors of two co-incident faces cancel, the theorem can be proved for arbitrary polyhedra!
A more sophisticated proof uses the divergence theorem from multivariable calculus: the component of each vector in the i direction is the flux of the constant vector field i across the closed surface, which by the divergence theorem is zero. The same is true in the j and k directions as well.
How to Cite this Page:
Su, Francis E., et al. “Polyhedral Face Vectors.” Math Fun Facts. <http://www.math.hmc.edu/funfacts>.
References:
S.J. Colley, Vector Calculus, Section 1.8.
Fun Fact suggested by:
Michael Moody

