Most of you know how to make a Mobius band—take a strip of paper and glue the ends with a half-twist. This object now has the property that is has only one “side”. It also has only one edge. Well, a disc has only one edge, too, so then we should be able to sew their edges together?
Indeed you can, although not in 3 dimensions (you’ll need at least 4 spatial dimensions to accomplish this). But after you are done, you will have a surface called a projective plane. An alternate way to construct a projective plane is to take a disc and sew pairs of opposite points together!
Does this object sound weird? Well, you are probably already familiar with projective planes… the old arcade version of the game of Asteroids was played on one! (Remember the screen was a disc, and when an asteroid hit one edge of the screen, it emerged on the opposite side of the screen? However, some have reported that the Atari home version of the game is played on a torus.)
Presentation Suggestions:
Draw pictures. Or take a piece of cloth shaped like a disc, take a zipper about half the length of the circumference, and sew both halves of the zipper onto the boundary of the disc. Then you should be able to sew up the disc at least part of the way…
The Math Behind the Fact:
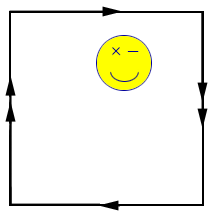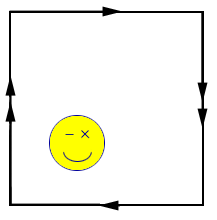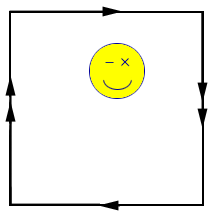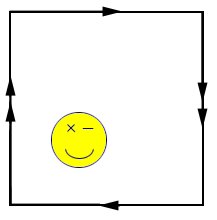
This is an example of a surface that is said to be non-orientable, because any two dimensional creature in the surface can walk along a path that will take it back to the original spot but the creature will be mirror-reversed! Look at what happens to the smiley face in Figure 1. Do you think that our universe is orientable?
How to Cite this Page:
Su, Francis E., et al. “Projective Planes.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
References:
J. Weeks, The Shape of Space.
Fun Fact suggested by:
Francis Su

