A regular polygon is a polygon whose angles are equal and side lengths are equal. A 3-D polyhedron is said to be regular if all its faces are regular polygons and the same number of faces meet at each corner. How many regular 3-D solid polyhedra are there?
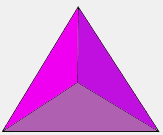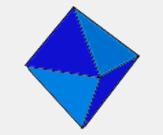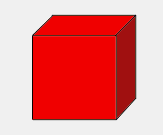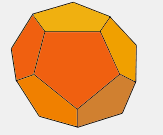
Answer: There are exactly five— the tetrahedron (pyramid with triangular faces), octahedron (8-sided with triangular faces), dodecahedron (12-sided with pentagonal faces), icosahedron (20-sided with triangular faces), and cube (6-sided with square faces).
These are sometimes called the Platonic Solids, named thus because they were described by Plato in one of his books. Euclid proved that there are only five.
Presentation Suggestions:
See if students can think of (or construct) some other polyhedra whose faces are the same shape, but allowing non-regular faces and/or different numbers of faces to meet at corners.
The Math Behind the Fact:
A regular solid with hexagonal faces cannot exist because if it did, the sum of the angles of any 3 hexagonal corners that meet would already equal 360, so such an object would be planar. Thus the only regular solids involve pentagons, squares, and triangular faces and you can further limit the possibilities using the Euler characteristic of the sphere, which is 2. This makes a great exercise.
How to Cite this Page:
Su, Francis E., et al. “Regular Solids.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
Fun Fact suggested by:
Francis Su

