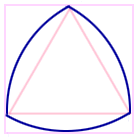
A Reuleaux Triangle is a plump triangle with rounded edges, formed in the following way: take the three points at the corners of an equilateral triangle, and connect each pair of points by a circular arc centered at the remaining point.
This triangle has some amazing properties. It is constant-width, meaning that it will hug parallel lines as it rolls. By rotating the centroid of the Reuleaux triangle appropriately, the figure can be made to trace out a square, perfect except for slightly rounded corners!
This idea has formed the basis of a drill that will carve out squares!
And, what do you think the ratio of its circumference to its width is?
Amazing fact: it is PI!
Presentation Suggestions:
Have students think about why this figure is constant width.
The Math Behind the Fact:
There are many other convex, constant-width figures, such as the circle and various Reuleaux polygons, and they all satisfy the same ratio of circumference to width!
How to Cite this Page:
Su, Francis E., et al. “Reuleaux Wheel.” Math Fun Facts. <http://www.math.hmc.edu/funfacts>.
Fun Fact suggested by:
Michael Moody

