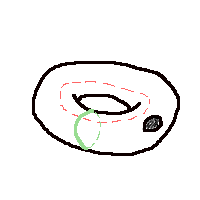
Consider a rubber tire (a torus) with a hole in it. Suppose that there is a green rubber band stuck to the outside of the torus that goes through the central cylinder, and a red rubber band pasted to the inside that stretches around the tire. So, if the tire were not there, the red and green rubber bands would be linked.
Suppose now that the tire is turned inside out through the hole. This is a continuous motion; so the red band is now on the outside, and the green on the inside. Moreover, it now seems as though the red and green rubber bands may be unlinked!
How can this be?
Presentation Suggestions:
Try this fun fact only if you can draw good pictures! Or, challenge students to try this with a physical model; try cutting and sewing ends of a sock.
The Math Behind the Fact:
You can resolve this paradox by actually turning the object inside out. What you find is that the red and blue rubber bands switch locations; in other words, the red band now runs through the central cylinder rather than around it. So there is no paradox; the rubber bands are still linked.
Take a topology course for more fun!
How to Cite this Page:
Su, Francis E., et al. “Rubber Bands Stuck on a Torus.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
Fun Fact suggested by:
Francis Su

