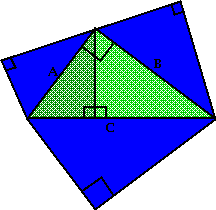
Here is one of the shortest proofs of the Pythagorean Theorem.
Suppose we are given any right triangle with sides of lengths A, B, C. In order to show that
A2 + B2 = C2
it is enough to show for any set of three similar figures whose widths relate to each other in the proportions A:B:C, that the area of the largest figure is the sum of the two smaller figures. This follows because area scales like the square of the width. The figures can be any shape.
So, let’s use the original triangle for the shape of the figures that we’ll use! Figure 1 shows that we’ve placed 3 blue triangles along the sides of the ABC right triangle so that their widths clearly relate to each other in the proportions A:B:C.
The two smaller blue triangles are congruent to the light and dark green right triangles, and the largest blue triangle is congruent to the entire ABC triangle. Since the sum of the areas of the green triangles equals the area of the ABC triangle, the sum of the areas of the smaller blue triangles equals the area of the largest blue triangle, as was to be shown!
Presentation Suggestions:
This is a lot easier to say than to write out in a Fun Fact file! It’s almost a proof without words!
The Math Behind the Fact:
Clever dissections of geometrical figures can give new insights! It is fun to try to think of new proofs to old theorems!
How to Cite this Page:
Su, Francis E., et al. “Shortest Pythagorean Proof?.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
Fun Fact suggested by:
Jorge Aarao

