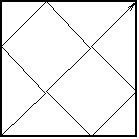
Consider a square in the plane. Is it possible to draw a curve in the square that touches every point inside the square? It seems that this should not be possible… after all, lines and planes are different dimensions.
Surprisingly, such a curve is possible! This counter-intuitive object is called a space-filling curve. You cannot draw it yourself, because it would take forever. However, it exists as the limit of a bunch of curves that you can draw.
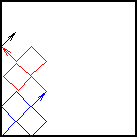
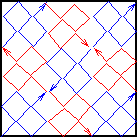
In the first stage draw a straight line from the lower left to upper right corner. In the second stage, replace that straight line by the zigzaggy curve in Figure 1. (By the way, the zigzaggy curve does meet itself at 2 places, but we’ve drawn them separate so you can resolve the curve.) Then, for every straight line segment in the second stage, replace it by a exact copy of the second stage, but scaled down by a 1/3 in each direction! See Figure 2 and Figure 3. Now repeat this process over and over, and the limiting object you obtain will be a continuous curve that fills the whole square!
Presentation Suggestions:
Of course, draw lots of pictures. Colored chalk may be helpful.
The Math Behind the Fact:
Which sets of curves “converge” to a continuous limiting curve is an issue tackled in a fun course called real analysis.
How to Cite this Page:
Su, Francis E., et al. “Space-filling Curves.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
Fun Fact suggested by:
Francis Su

