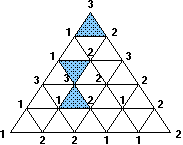
Divide a triangle T into lots of baby triangles, so that baby triangles only meet at a common edge or a common vertex. Label each main vertex of the whole triangle by 1, 2, or 3; then label vertices on the (12) side by either 1 or 2, on the (23) side by either 2 or 3, and the (13) side by either 1 or 3. Label the points in the interior by any of 1, 2, or 3. For instance, see Figure 1.
Fun Fact: any such labelling must contain an baby (123) triangle! (In fact, there must be an odd number!)
Actually, a version of Sperner’s Lemma holds in all dimensions. Can you figure out how it generalizes?
Sperner’s Lemma is equivalent to the Brouwer fixed point theorem.
Presentation Suggestions:
Have everyone make their own labelled triangle and see how many (123) triangles they have in their picture.
The Math Behind the Fact:
There are many proofs of this fact. Some short non-constructive proofs rely on parity arguments. Constructive proofs are the key to many fixed point algorithms as well as fair division procedures. See the reference.
How to Cite this Page:
Su, Francis E., et al. “Sperner’s Lemma.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
References:
F.E. Su, “Rental harmony: Sperner’s lemma in fair division”,
Amer. Math. Monthly, 1999.
Fun Fact suggested by:
Francis Su

