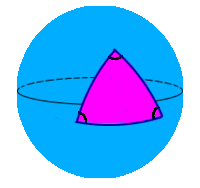
Remember high school geometry? The sum of the angles of a planar triangle is always 180 degrees or Pi radians. However, triangles on other surfaces can behave differently!
For instance, consider a triangle on a sphere, whose edges are “intrinsically” straight in the sense that if you were a very tiny ant living on the sphere you would not think the edges were bending either to the left or right. (Such intrinsically straight lines are called geodesics. On spheres, they correspond to pieces of great circles whose center coincide with the center of the sphere.)
A triangle on a sphere has the interesting property that the sum of the angles is greater than 180 degrees! And in fact, two triangles with the same angles are not just similar (as in planar geometry), they are actually congruent! But wait, there’s more: on a UNIT sphere, the AREA of the triangle actually satisfies:
AREA of a triangle = (sum of angles) – Pi ,
where the angles are measured in radians. Cool!
Another neat fact about spherical triangles may be found in Spherical Pythagorean Theorem.
Presentation Suggestions:
Demonstrate the assertions about angles and areas with an example: draw a picture of a sphere and then draw a triangle whose vertices are at the north pole and at two distinct points on the equator. Here’s a follow-up question for your students: are geodesic paths always the shortest paths between two points?
The Math Behind the Fact:
Planar geometry is sometimes called flat or Euclidean geometry. The geometry on a sphere is an example of a spherical or elliptic geometry. Another kind of non-Euclidean geometry is hyperbolic geometry. Spherical and hyperbolic geometries do not satisfy the parallel postulate.
By the way, 3-dimensional spaces can also have strange geometries. Our universe, for instance, seems to have a Euclidean geometry on a local scale, but does not on a global scale. In much the same way that a sphere is “curved”, so that divergent geodesics extending from the south pole will meet again at the north pole, Einstein suggested that 3-space is “curved” by the presence of matter, so that light rays (which follow geodesics) bend near very massive objects!
How to Cite this Page:
Su, Francis E., et al. “Spherical Geometry.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
References:
J. Weeks, The Shape of Space.
Fun Fact suggested by:
Francis Su

