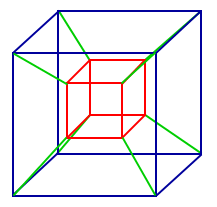
What does a cube look like in higher dimensions?
Well, we can extrapolate by looking at lower dimensions.
A 0-dimensional cube is a point, a vertex.
A 1-dimensional “cube” is a line segment, with 2 vertices at either end. It is obtained from a 0-dimensional cube by thickening it in one dimension.
A 2-dimensional “cube” is square, with 4 vertices, obtained by thickening up the line segment in a second dimension.
A 3-dimensional “cube” is a cube, with 8 vertices, obtained from the square by thickening it in a third dimension.
So, by extrapolation the 4-dimensional “cube”, also called a tesseractor hypercube, should have 16 vertices, and is obtained from a cube by thickening it up in a fourth dimension. Since we cannot easily visualize this, there are a number of ways we can understand this object by viewing projections, or “shadows” of it in 3-D. See Figure 1.
Presentation Suggestions:
See if students can guess by extrapolation how many vertices the tesseract should have.
The Math Behind the Fact:
Thinking in four dimensions is not easy, and takes practice. However, a number of science fiction books have been written around this idea and explain it and possible applications quite well; see the reference for one notable example.
How to Cite this Page:
Su, Francis E., et al. “Tesseract.” Math Fun Facts. <http://www.math.hmc.edu/funfacts>.
References:
M. L’Engle, A Wrinkle in Time.
Fun Fact suggested by:
Francis Su

