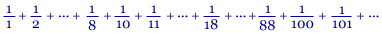
You’re probably already aware that the harmonic series, which is the sum of the reciprocals of all natural numbers, diverges. In fact, it diverges if you take away every other term. It even diverges if you take away nine out of every ten terms.
So, what do you think would happen if we tried to take the sum of reciprocals of all natural numbers that do not contain the number nine (when written in decimal expansion)?
Amazingly, this series converges!
Presentation Suggestions:
Write out the first several terms. Allow students to guess whether or not this converges. For instance, it may appear that this series is divergent, especially when contrasting it with sums of reciprocals of numbers with one or more 9’s. That series diverges (easy to show), and this series seems to have “more” terms in it…
The Math Behind the Fact:
Group the terms based on the number of digits in their denominator. There are 8 terms in (1/1+…+ 1/8) each of which is no larger than 1. Consider the next group (1/10+…+1/88). The number of terms is at most the number of ways to choose two ordered digits out of the digits 0..8, and each such term is clearly no larger than 1/10. So this group’s sum is no larger than 92/10. Similarly, the sum of the terms in (1/100+…+1/999) is at most 93/102, etc.
So the entire sum is no larger than
9*1 + 9*(9/10) + 9*(92/102) + … + 9*(9n/10n) + …
This a geometric series that converges. Thus by the comparison test, the original sum (which is smaller term-by-term) must converge!
How to Cite this Page:
Su, Francis E., et al. “Thinned-Out Harmonic Series.” Math Fun Facts. <https://www.math.hmc.edu/funfacts>.
References:
G.H. Behforooz, “Thinning out the Harmonic Series”, Math. Mag., vol. 68, number 4, October 1995.
Fun Fact suggested by:
Dominic Mazzoni

