How many rational numbers are there? Yes, infinitely many, I hear you say. But how large is that infinity? Are...
Continue reading...analysis
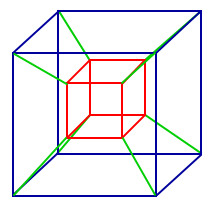
Volume of a Ball in N Dimensions
The unit ball in Rn is defined as the set of points (x1,…,xn) such that x12 + … + xn2 <= 1. What...
Continue reading...Sphere Eversions
If you take a loop of string in the plane and place an arrow along it pointing clockwise, is it...
Continue reading...Taylor-made Pi
After learning about the Taylor series for 1/(1+x) in calculus, you can find an interesting expression for Pi very easily. Start with...
Continue reading...Banach-Tarski Paradox
Did you know that it is possible to cut a solid ball into 5 pieces, and by re-assembling them, using...
Continue reading...i to the i is a Real Number
If you are familiar with complex numbers, the “imaginary” number i has the property that the square of i is -1....
Continue reading...Face Derivatives and Computer Vision
One challenge in robotics is the problem of computer vision: how do you program a computer to interpret and “understand”...
Continue reading...Ellipsoidal Paths
Given an ellipse, and a smaller ellipse strictly inside it, start at a point on the outer ellipse, and in a...
Continue reading...Whiffle Ball
Does a ball take longer to come down than go up, or does it take the same amount of time...
Continue reading...Area of a Circle or Regular Polygon
There’s a nice way to see why the formula for the area of a circle of radius R is: Pi...
Continue reading...